前回、カグルのこれ『Pokemon with stats』を使って、『【kaggle】ポケモンデータでlightGBMしてみる』これをやり、伝説ポケモンたらしめているデータは何なのか、を見ていきました。今回は、基本的な統計(HP、攻撃、防御、特殊攻撃、特殊防御、速度等)情報がまとまっているので、これらを用いて、k平均法(クラスタリング)をやっていこうと思います。立春に。
データの準備
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use("ggplot")いつものやつをインポート。
df=pd.read_csv("/content/drive/MyDrive/Colab Notebooks/Pokemon.csv")
df.head(10) データフレームとして読み込んで表示、これは前回と同じです。
| # | Name | Type 1 | Type 2 | Total | HP | Attack | Defense | Sp. Atk | Sp. Def | Speed | Generation | Legendary | |
| 0 | 1 | Bulbasaur | Grass | Poison | 318 | 45 | 49 | 49 | 65 | 65 | 45 | 1 | FALSE |
| 1 | 2 | Ivysaur | Grass | Poison | 405 | 60 | 62 | 63 | 80 | 80 | 60 | 1 | FALSE |
| 2 | 3 | Venusaur | Grass | Poison | 525 | 80 | 82 | 83 | 100 | 100 | 80 | 1 | FALSE |
| 3 | 3 | VenusaurMega Venusaur | Grass | Poison | 625 | 80 | 100 | 123 | 122 | 120 | 80 | 1 | FALSE |
| 4 | 4 | Charmander | Fire | NaN | 309 | 39 | 52 | 43 | 60 | 50 | 65 | 1 | FALSE |
| 5 | 5 | Charmeleon | Fire | NaN | 405 | 58 | 64 | 58 | 80 | 65 | 80 | 1 | FALSE |
| 6 | 6 | Charizard | Fire | Flying | 534 | 78 | 84 | 78 | 109 | 85 | 100 | 1 | FALSE |
| 7 | 6 | CharizardMega Charizard X | Fire | Dragon | 634 | 78 | 130 | 111 | 130 | 85 | 100 | 1 | FALSE |
| 8 | 6 | CharizardMega Charizard Y | Fire | Flying | 634 | 78 | 104 | 78 | 159 | 115 | 100 | 1 | FALSE |
| 9 | 7 | Squirtle | Water | NaN | 314 | 44 | 48 | 65 | 50 | 64 | 43 | 1 | FALSE |
HPからSpeedまでのデータでやっていきます。
x=df.iloc[:,5:11]k平均法はデータの距離を扱うので、標準化します。
from sklearn.preprocessing import StandardScaler
scaler=StandardScaler()
x_std=scaler.fit_transform(x)データの準備はこれで整いました。
エルボー(肘)法
k平均法では、クラスタ数はハイパーパラメータで人間が決めなければいけません。妥当なクラスタ数を見つける手段として、エルボー(肘)法を使います。
from sklearn.cluster import KMeans
sum = []
for i in range(1,11):
km=KMeans(n_clusters=i)
km.fit(x_std)
sum.append(km.inertia_)
plt.figure(figsize=(10,10))
plt.plot(range(1,11),sum,marker='o',color="blue",ms=15)
plt.xlabel("cluster")
plt.ylabel("sum")
plt.show()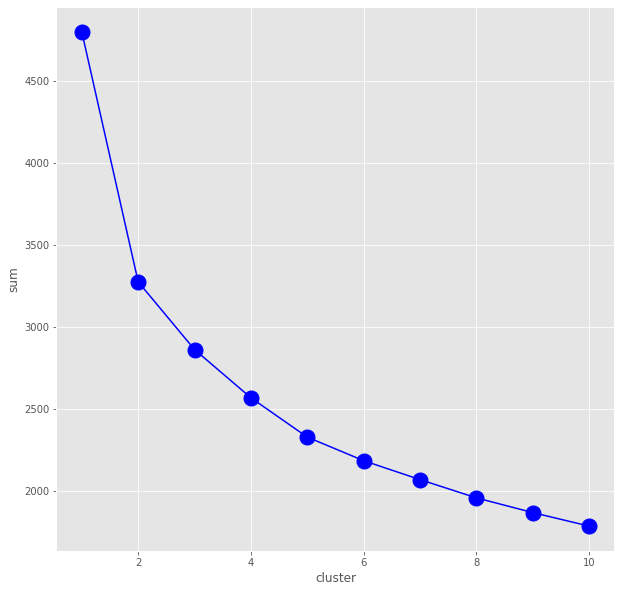
sumは各重心からデータまでの距離の総和で、横軸はクラスタ数です。このグラフの傾きの変化が大きいところ(肘みたいに折れてる)が、距離の総和の減り具合が減る(傾き増える)ので妥当なクラスタ数だろう、というわけです。が、2じゃん。。。
よく見ると、うっすら5にも肘出てるので、クラスタ数5でやってみようと思います。
k平均法で学習
k_means=KMeans(n_clusters=5).fit(x_std)学習はこれでおしまい!便利!
結果をザっとみると、
k_means.labels_array([1, 3, 3, 2, 1, 3, 3, 2, 2, 1, 3, 4, 2, 1, 1, 3, 1, 1, 3, 3, 1, 1,
3, 2, 1, 3, 1, 3, 1, 3, 1, 3, 1, 4, 1, 1, 0, 1, 1, 3, 1, 0, 1, 3,
1, 0, 1, 3, 1, 1, 0, 1, 4, 1, 3, 1, 3, 1, 3, 1, 3, 1, 3, 1, 2, 1,
3, 0, 1, 3, 3, 2, 1, 0, 0, 1, 1, 3, 1, 3, 1, 4, 4, 3, 3, 1, 0, 4,
1, 3, 1, 1, 3, 1, 0, 1, 0, 1, 4, 1, 3, 3, 2, 4, 1, 0, 1, 4, 1, 3,
1, 0, 1, 4, 3, 4, 0, 1, 4, 1, 0, 0, 4, 0, 2, 1, 3, 1, 3, 1, 3, 3,
3, 3, 3, 3, 3, 2, 3, 1, 0, 2, 0, 1, 1, 0, 3, 2, 1, 1, 4, 1, 4, 3,
2, 0, 2, 2, 2, 1, 3, 2, 2, 2, 2, 2, 1, 3, 4, 1, 3, 3, 1, 3, 0, 1,
3, 1, 0, 1, 3, 1, 1, 3, 1, 0, 1, 1, 1, 1, 4, 1, 3, 1, 1, 0, 2, 4,
1, 0, 4, 0, 1, 1, 3, 1, 1, 0, 3, 1, 0, 3, 4, 3, 0, 3, 1, 0, 3, 1,
4, 0, 3, 4, 4, 1, 0, 3, 4, 4, 4, 3, 4, 3, 1, 0, 1, 4, 1, 0, 4, 1,
0, 1, 3, 4, 1, 3, 2, 2, 1, 4, 0, 3, 1, 1, 4, 1, 3, 3, 3, 0, 2, 2,
2, 1, 3, 2, 2, 2, 2, 2, 1, 3, 3, 2, 1, 3, 2, 2, 1, 3, 0, 2, 1, 3,
1, 3, 1, 1, 3, 1, 1, 1, 1, 3, 1, 1, 3, 1, 3, 1, 4, 1, 1, 3, 2, 1,
3, 1, 3, 1, 3, 2, 1, 3, 1, 1, 1, 0, 1, 0, 1, 4, 1, 1, 1, 4, 1, 4,
1, 4, 4, 4, 1, 3, 3, 1, 3, 2, 3, 3, 3, 3, 3, 1, 0, 1, 3, 2, 0, 0,
1, 0, 2, 4, 1, 3, 1, 1, 1, 3, 1, 3, 1, 3, 2, 3, 3, 3, 3, 1, 0, 1,
3, 1, 4, 1, 4, 1, 4, 1, 0, 3, 4, 1, 3, 2, 1, 4, 0, 3, 3, 2, 1, 1,
3, 2, 1, 0, 0, 1, 4, 4, 4, 1, 1, 4, 2, 2, 1, 4, 2, 2, 4, 4, 4, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 4, 3, 1, 0, 0, 1, 3, 3, 1, 3,
0, 1, 1, 3, 1, 3, 1, 1, 1, 1, 2, 1, 3, 1, 0, 4, 4, 1, 4, 4, 4, 3,
1, 4, 3, 1, 3, 1, 3, 1, 0, 3, 1, 0, 1, 3, 2, 3, 0, 1, 3, 1, 1, 0,
1, 4, 1, 1, 1, 3, 4, 1, 3, 2, 2, 0, 1, 3, 2, 1, 0, 1, 3, 1, 3, 0,
1, 3, 1, 1, 0, 2, 3, 4, 0, 0, 0, 2, 2, 2, 3, 4, 4, 4, 0, 2, 3, 2,
4, 4, 3, 3, 4, 4, 4, 4, 4, 4, 2, 2, 2, 2, 2, 2, 2, 2, 0, 3, 2, 2,
2, 2, 2, 2, 1, 3, 3, 1, 0, 0, 1, 3, 0, 1, 3, 1, 1, 0, 1, 3, 1, 3,
1, 3, 1, 3, 1, 0, 1, 1, 3, 1, 3, 1, 4, 4, 1, 3, 1, 0, 0, 4, 1, 0,
0, 1, 3, 0, 0, 3, 1, 4, 3, 1, 4, 3, 1, 3, 1, 3, 3, 1, 1, 3, 1, 0,
0, 3, 1, 4, 1, 4, 3, 1, 4, 1, 4, 3, 2, 1, 3, 1, 3, 1, 3, 1, 1, 4,
1, 1, 0, 1, 3, 1, 3, 2, 1, 3, 3, 1, 4, 1, 0, 1, 0, 0, 1, 3, 1, 4,
1, 4, 4, 1, 1, 0, 1, 0, 1, 1, 3, 1, 3, 3, 1, 0, 3, 1, 3, 0, 1, 3,
4, 1, 0, 1, 4, 0, 1, 0, 1, 0, 0, 3, 1, 3, 2, 1, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 1, 4, 4, 1, 3, 3, 1, 3,
3, 1, 3, 1, 3, 3, 1, 1, 3, 1, 3, 1, 1, 2, 1, 0, 1, 0, 3, 1, 3, 3,
1, 4, 2, 4, 1, 0, 1, 3, 1, 0, 1, 4, 1, 4, 1, 3, 1, 3, 1, 4, 1, 0,
0, 3, 3, 4, 1, 3, 2, 3, 1, 0, 1, 1, 1, 1, 4, 4, 4, 4, 1, 4, 1, 3,
2, 2, 2, 4, 2, 2, 2, 2], dtype=int32)こんな感じで、5つのクラスタ分けができました。
結果の読み解き
重心とデータの近さで機械がクラスタリングしてくれたわけですが、その意味するところは人が読み解いていかなあきません。それをやっていきます。
x_std=np.round(x_std,2)
x_std見やすいように、丸めます。
array([[-0.95, -0.92, -0.8 , -0.24, -0.25, -0.8 ],
[-0.36, -0.52, -0.35, 0.22, 0.29, -0.29],
[ 0.42, 0.09, 0.29, 0.83, 1.01, 0.4 ],
...,
[ 0.42, 0.96, -0.44, 2.36, 2.09, 0.06],
[ 0.42, 2.5 , -0.44, 2.97, 2.09, 0.4 ],
[ 0.42, 0.96, 1.48, 1.75, 0.65, 0.06]])x_std=pd.DataFrame(x_std)
x_std.columns=x.columns
x_std.head()標準化の際にndarray型になったx_stdをdataframe型に戻します。
| HP | Attack | Defense | Sp. Atk | Sp. Def | Speed | |
| 0 | -0.95 | -0.92 | -0.8 | -0.24 | -0.25 | -0.8 |
| 1 | -0.36 | -0.52 | -0.35 | 0.22 | 0.29 | -0.29 |
| 2 | 0.42 | 0.09 | 0.29 | 0.83 | 1.01 | 0.4 |
| 3 | 0.42 | 0.65 | 1.58 | 1.5 | 1.73 | 0.4 |
| 4 | -1.19 | -0.83 | -0.99 | -0.39 | -0.79 | -0.11 |
これに学習結果を追加します。
x_std["labels"]=k_means.labels_さらに、名前をくっつけて、
pkresults=pd.concat([df["Name"],x_std],axis=1)
pkresults| Name | HP | Attack | Defense | Sp. Atk | Sp. Def | Speed | labels | |
| 0 | Bulbasaur | -0.95 | -0.92 | -0.8 | -0.24 | -0.25 | -0.8 | 0 |
| 1 | Ivysaur | -0.36 | -0.52 | -0.35 | 0.22 | 0.29 | -0.29 | 3 |
| 2 | Venusaur | 0.42 | 0.09 | 0.29 | 0.83 | 1.01 | 0.4 | 3 |
| 3 | VenusaurMega Venusaur | 0.42 | 0.65 | 1.58 | 1.5 | 1.73 | 0.4 | 2 |
| 4 | Charmander | -1.19 | -0.83 | -0.99 | -0.39 | -0.79 | -0.11 | 0 |
| … | … | … | … | … | … | … | … | … |
| 795 | Diancie | -0.75 | 0.65 | 2.44 | 0.83 | 2.81 | -0.63 | 4 |
| 796 | DiancieMega Diancie | -0.75 | 2.5 | 1.16 | 2.67 | 1.37 | 1.44 | 2 |
| 797 | HoopaHoopa Confined | 0.42 | 0.96 | -0.44 | 2.36 | 2.09 | 0.06 | 2 |
| 798 | HoopaHoopa Unbound | 0.42 | 2.5 | -0.44 | 2.97 | 2.09 | 0.4 | 2 |
| 799 | Volcanion | 0.42 | 0.96 | 1.48 | 1.75 | 0.65 | 0.06 | 2 |
ひとまず、データがまとまりました。
これをさらにクラスタごとに分けて、HPからSpeedの平均値を見ていきます。
pk_0=pkresults[pkresults["labels"]==0]
pk_1=pkresults[pkresults["labels"]==1]
pk_2=pkresults[pkresults["labels"]==2]
pk_3=pkresults[pkresults["labels"]==3]
pk_4=pkresults[pkresults["labels"]==4]まずは、0クラス
plt.figure(figsize=(10,10))
plt.bar(pk_0.iloc[:,1:7].columns,pk_0.iloc[:,1:7].mean(),color="blue")
plt.ylim(-0.9,1.7)
plt.xlabel("columns")
plt.ylabel("values")
plt.show()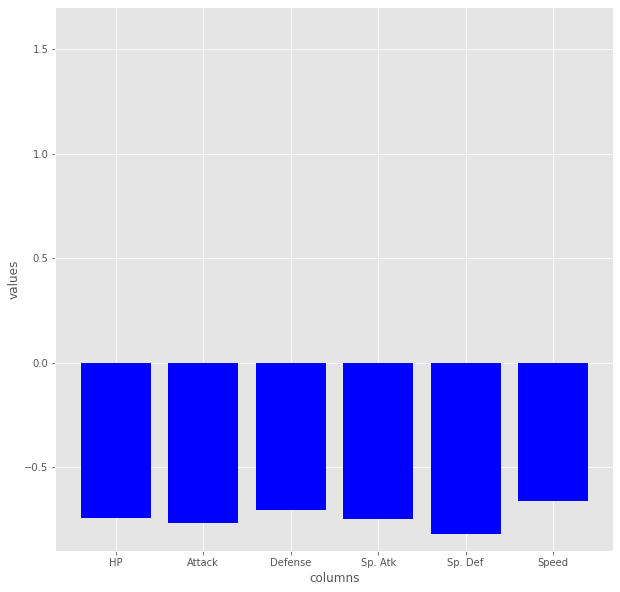
283種が該当してますが、これはどうみても弱いポケモングループですね。
次、1クラス(以下、先とほぼ同じコードなので省略します)
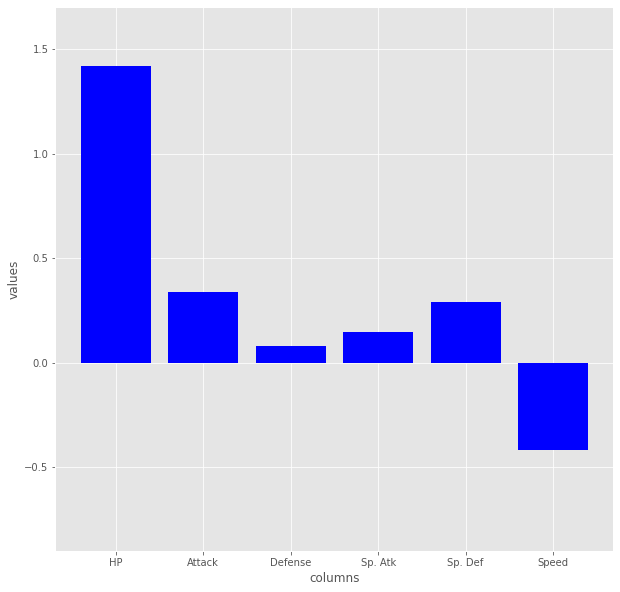
102種が該当です、これはHPオバケ遅い遅いグループですね。
次、2クラス
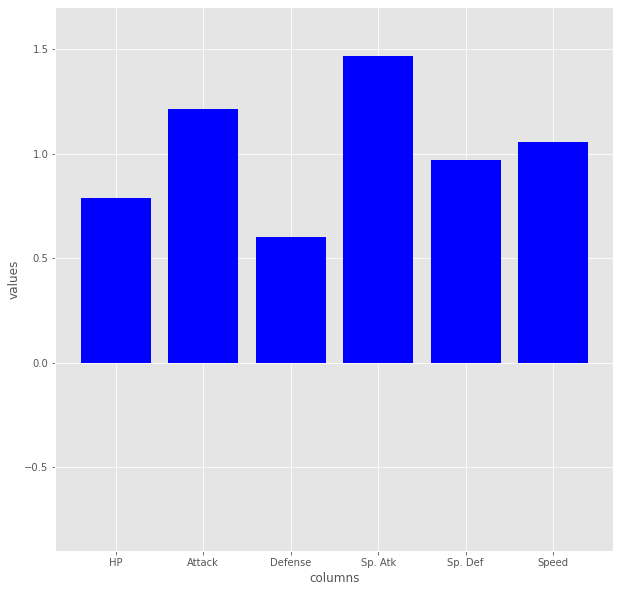
118種該当、明らかにバランスよく強いグループですね。前回の記事を踏まえると、伝説ポケモンがここにうじゃうじゃいるんでしょう。
次、3クラス
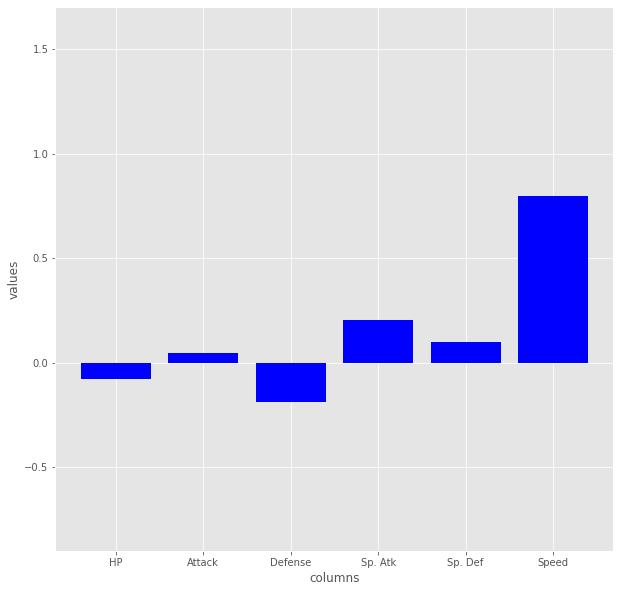
202種該当、ちょこまか逃げて特攻でがんばるグループ。
最後、4クラス
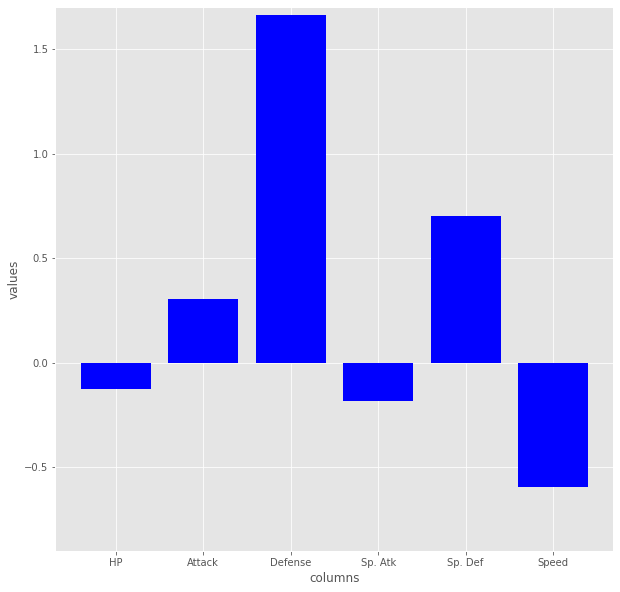
95種該当、かったいおっそいグループ。
まとめるとこんな感じ、
| 数 | 割合 | |
| 弱いポケモン | 283 | 35.4% |
| HPオバケ遅い遅い | 102 | 12.8% |
| バランスよく強い | 118 | 14.8% |
| ちょこまか逃げて特攻でがんばる | 202 | 25.3% |
| かったいおっそい | 95 | 11.9% |
| 計 | 800 | 100% |
肘がうっすらだったので、どうかしらんと思ってたんですが、結構わかりやすいクラスタになってくれました。


