前回『決定木の予測平面を描画してみる①』の続編で、もう少しやっていきたいと思います。それでは、いってみましょう。
ハイパーパラメータの変更
| max_depth | 木の最大の深さ | 3 |
| min_samples_leaf | 葉に入る最小のデータ数 | 20 |
前回はこれだったので、当然シンプルな(分割領域の少ない)予測平面となったのですが、
| max_depth | 木の最大の深さ | 5 |
| min_samples_leaf | 葉に入る最小のデータ数 | 20 |
これでも見ておきましょう。
tree=DecisionTreeClassifier(max_depth=5,min_samples_leaf=20).fit(x,y)こうして、ディシジョンツリークラシファイアー!!!
前回同様描画します。
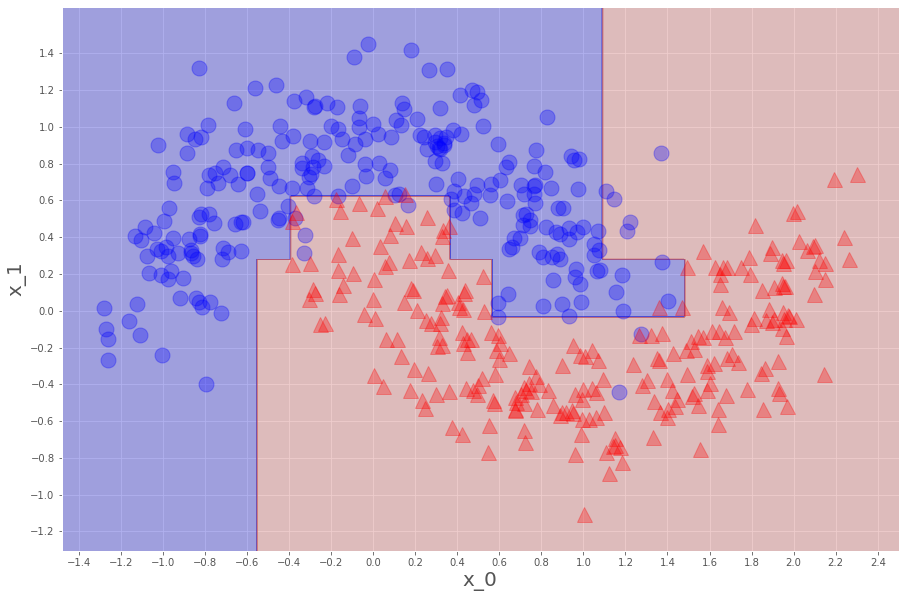
分割領域が増えて、よりデータにフィットする形になってくれました。
正解率も、0.972と上がっています。
多値(多クラス、多ラベル)を扱う
ここまでは2値のデータだったわけですが、当然多値も見てみたくなりますよね。ということでサイキットラーン/データ生成やらで調べると、当たり前のようにありました、メイクブロブズ。
x,y=make_blobs(n_samples=500,n_features=2,centers=7,random_state=0)| n_samples | 生成するデータの数 | 500 |
| n_features | 特徴量の数 | 2 |
| centers | データの塊の数 | 7 |
| random_state | 乱数の出し方を固定 | 0 |
関数を作って描画するとこんな感じ。
def plot_datasets(x,y):
plt.plot(x[:,0][y==0],x[:,1][y==0],"o",c="blue",ms=15,alpha=0.2)
plt.plot(x[:,0][y==1],x[:,1][y==1],"^",c="red",ms=15,alpha=0.2)
plt.plot(x[:,0][y==2],x[:,1][y==2],"s",c="green",ms=15,alpha=0.2)
plt.plot(x[:,0][y==3],x[:,1][y==3],"d",c="purple",ms=15,alpha=0.2)
plt.plot(x[:,0][y==4],x[:,1][y==4],"*",c="darkblue",ms=15,alpha=0.2)
plt.plot(x[:,0][y==5],x[:,1][y==5],">",c="orange",ms=15,alpha=0.2)
plt.plot(x[:,0][y==6],x[:,1][y==6],"p",c="black",ms=15,alpha=0.2)
plt.xlabel("x_0",fontsize=20)
plt.ylabel("x_1",fontsize=20)
plt.figure(figsize=(15,10))
plot_datasets(x,y)
plt.show()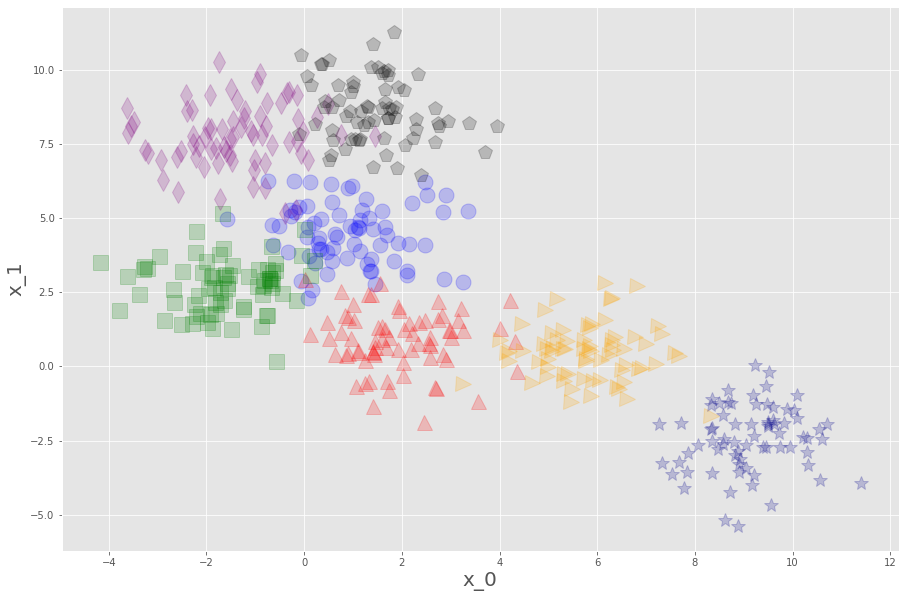
ということで、7つのラベルを持つ、予測平面として分割しがいのあるデータがプロットできました。
なのでこいつはランダムフォレストでもやってみたいと思います。
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier
tree=DecisionTreeClassifier(max_depth=5,min_samples_leaf=10).fit(x,y)
rtree=RandomForestClassifier(n_estimators=200,max_depth=5,min_samples_leaf=10).fit(x,y)ランダムフォレスト
・木を何本もはやす
・1本の木が扱うデータをランダムにとる
・全部の木の予測結果の平均を最終的な予測結果とする
というやつで、 n_estimatorsで木の本数を指定しています。
学習できたので、正解率を確認、
print(tree.score(x,y))
print(rtree.score(x,y))
0.936
0.95若干ランダムフォレストの方がいいですね、さて、どんな予測平面になってるんでしょうか。
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf,x,m=0.2):
_x0=np.linspace(x[:,0].min()-m,x[:,0].max()+m,500)
_x1=np.linspace(x[:,1].min()-m,x[:,1].max()+m,500)
x0,x1=np.meshgrid(_x0,_x1)
x_new=np.c_[x0.ravel(),x1.ravel()]
y_pred=clf.predict(x_new).reshape(x1.shape)
cmap=ListedColormap(["mediumblue","indianred","greenyellow",
"rebeccapurple","blueviolet","orangered","grey"])
plt.contourf(x0,x1,y_pred,alpha=0.3,cmap=cmap)
plt.figure(figsize=(22,10))
plt.subplot(121)
plot_decision_boundary(tree,x)
plot_datasets(x,y)
plt.subplot(122)
plot_decision_boundary(rtree,x)
plot_datasets(x,y)
plt.show()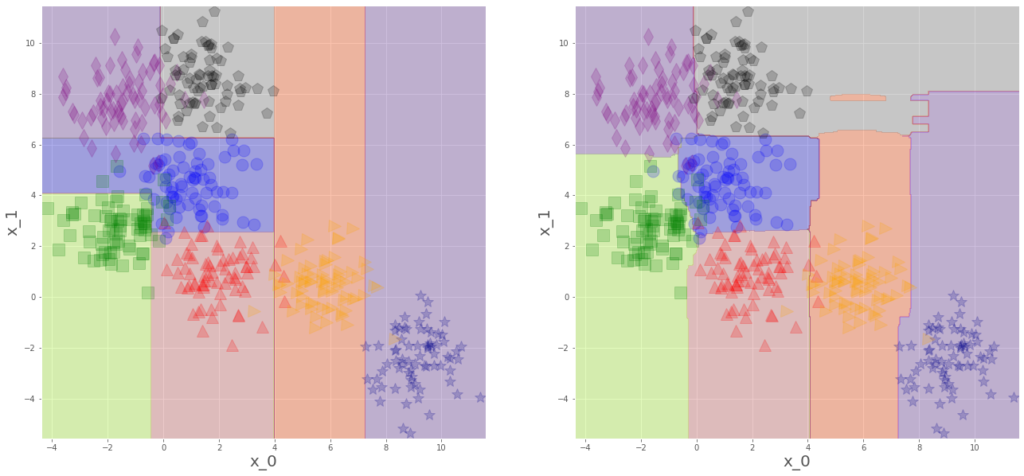
7ラベルだろうが、きちんと頑張って予測平面を作ってくれました。
右がランダムフォレストですが、ランダム平均パワーで正解となる領域を増やしてくれていることがわかります。


