今回は、タイトルの通り2次元データを用いて決定木の予測平面を描画したいと思います。
それでは、いってみましょう。
ライブラリをインポート
import numpy as np
import matplotlib.pyplot as plt
plt.style.use("ggplot")
そうです、この世界では、まずはこれからです。ナムパイとマットプロットリブをインポート。しかし、この界隈のライブラリの名前は、なんだかとてもかっこいい。
スタイルも冒頭で指定しています。
データの準備
from sklearn.datasets import make_moonsサイキットラーンのデータセッツから、メイクムーンズをインポート。
ほんと、どれもこれもかっこいい。
2次元に2値のデータをプロットしたいので、メイクムーンズを用います。
x,y=make_moons(n_samples=500,noise=0.2,random_state=0)| n_samples | 生成するデータの数 | 500 |
| noise | データのばらつき具合 | 0.2 |
| random_state | 乱数の出し方を固定 | 0 |
としています。関数を定義してデータをプロットすると
def plot_datasets(x,y):
plt.plot(x[:,0][y==0],x[:,1][y==0],"o",c="blue",ms=15,alpha=0.3)
plt.plot(x[:,0][y==1],x[:,1][y==1],"^",c="red",ms=15,alpha=0.3)
plt.xticks( np.arange(-1.4,2.5,0.2))
plt.yticks( np.arange(-1.2,1.6,0.2))
plt.xlabel("x_0",fontsize=20)
plt.ylabel("x_1",fontsize=20)
plt.figure(figsize=(15,10))
plot_datasets(x,y)
plt.show()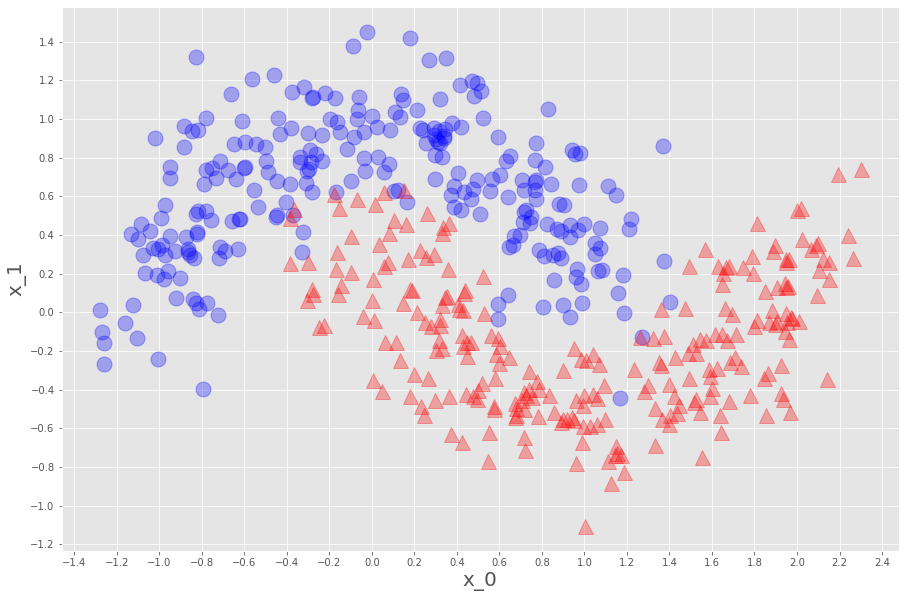
こんな感じ。これでデータの準備ができました。
学習と予測平面の描画
さて、これがやりたかったことです。決定木をインポートして、先のデータを学習させます。
from sklearn.tree import DecisionTreeClassifier
tree=DecisionTreeClassifier(max_depth=3,min_samples_leaf=20).fit(x,y)
ディシジョンツリークラシファイアー!!ですよ、火がでる必殺技以外の意味があるんでしょうか。
| max_depth | 木の最大の深さ | 3 |
| min_samples_leaf | 葉に入る最小のデータ数 | 20 |
ひとまずこれで。
しかし、書いてて思いましたけど、【木】なんだったら【深さ】じゃなくて【長さ】だし、
分岐を下に延ばして書いていくので、【木】じゃなくて【根】じゃね?
そうすると【葉】の表現ができないから、【木】にしたのか。。。?
だったら、【アリの巣】みたいな表現の方が…………ここまでにしましょう。
これで学習できたので、描画します!
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf,x,m=0.2):
_x0=np.linspace(x[:,0].min()-m,x[:,0].max()+m,500)
_x1=np.linspace(x[:,1].min()-m,x[:,1].max()+m,500)
x0,x1=np.meshgrid(_x0,_x1)
x_new=np.c_[x0.ravel(),x1.ravel()]
y_pred=clf.predict(x_new).reshape(x1.shape)
cmap=ListedColormap(["mediumblue","indianred"])
plt.contourf(x0,x1,y_pred,alpha=0.3,cmap=cmap)
予測平面を描画する関数を定義。
これ、 linspaceとmeshgridとc_とravelとreshapeとcontourfで何やってるかがわかると理解できます。 全部ですね。
そして、データプロットした関数と合わせて、こう。
plt.figure(figsize=(15,10))
plot_decision_boundary(tree,x)
plot_datasets(x,y)
plt.show()で、こう。
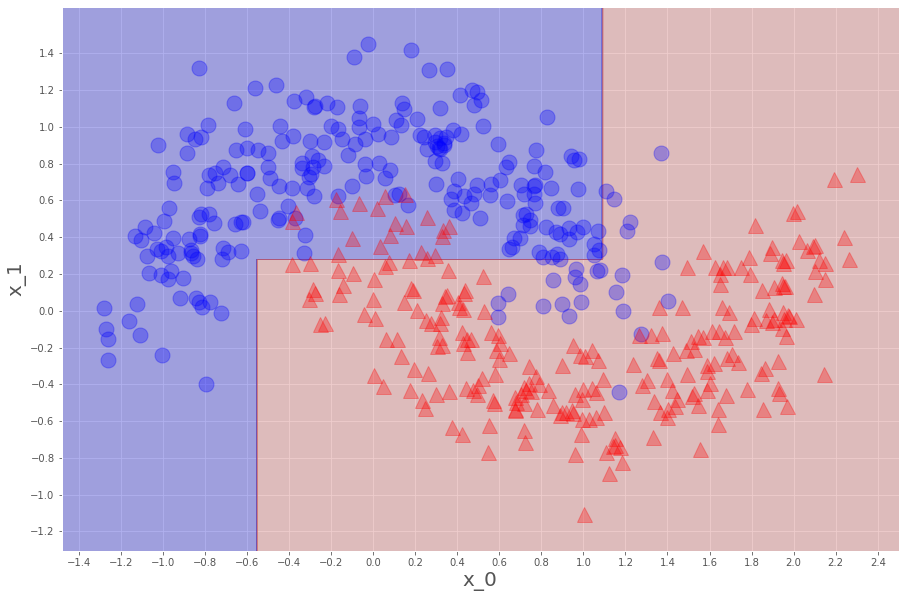
先のハイパーパラメータの条件で、500個の教師データからこのような分類器ができました。
つまり、未知のデータが青(赤)領域なら、0(1)と判断する分類器ですね。
学習データに対する正解率は、
print(tree.score(x,y))0.908
コンピュータがやってくれたのは、こういうこと。
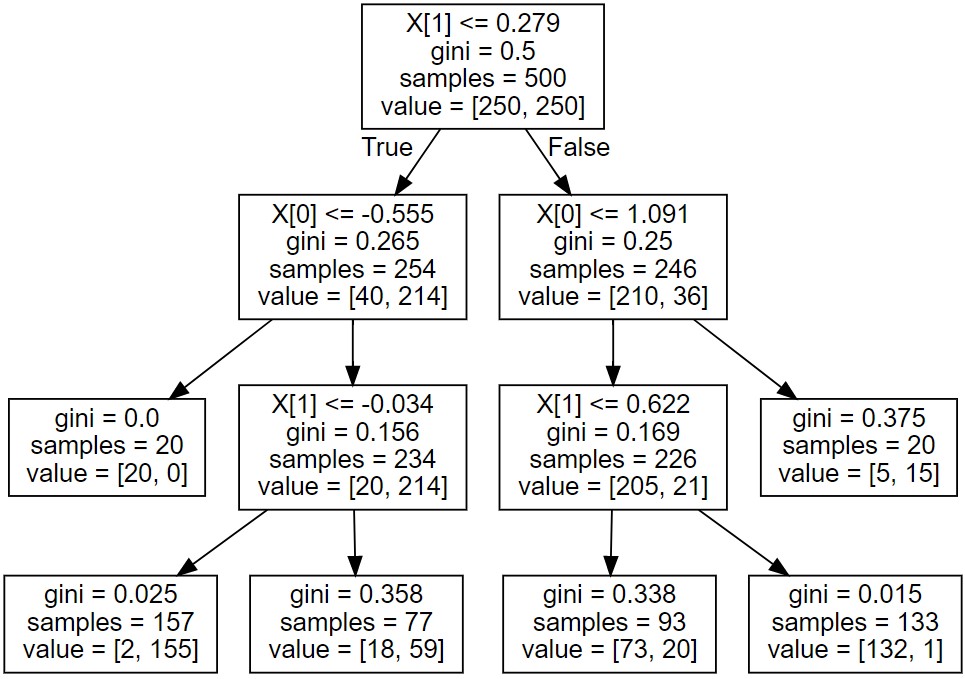
やっぱりこれって【アリの巣】で、一番上がholeで、各roomとか言う方が、失礼。
ジニ不純度を最も下げる境界を計算して見つけだし、深さ3まで分岐を続け(平面を6つに割って)、各領域に多くある方(0のデータか1のデータか)を、各々青(0)エリア赤(1)エリアに分けてくれています。
めちゃくちゃわかりずらい文章

