さて、前回『決定木の予測平面を描画してみる② 』、多値でのケースも見てみたのですが、言うて7つの塊が置いてるだけ―、なので
もうちょっと複雑な分布が欲しくなります。なりました。
そこで、また、サイキットラーンデータセッツをまさぐると、やっぱりあるんですよ。
メイクガウシャンクオンタイルズです。
データの準備
先の公式サイトを見ると、
・多次元の標準化(分散:1、平均:0)された正規分布に従うデータを出すよ
・同心円で各データにラベルつけるけど、各ラベルのデータ数がほぼ同じになるようにするよ
ってなことらしい、百聞は一見に如かずだから、また特徴量2個でプロットしてみる。
import numpy as np
import matplotlib.pyplot as plt
plt.style.use("ggplot")
from sklearn.datasets import make_gaussian_quantiles
x,y=make_gaussian_quantiles(cov=20,n_samples=500,n_features=2,n_classes=3,random_state=10)
def plot_datasets(x,y):
plt.plot(x[:,0][y==0],x[:,1][y==0],"o",c="blue",ms=15,alpha=0.2)
plt.plot(x[:,0][y==1],x[:,1][y==1],"^",c="red",ms=15,alpha=0.2)
plt.plot(x[:,0][y==2],x[:,1][y==2],"s",c="green",ms=15,alpha=0.2)
plt.xlabel("x_0",fontsize=20)
plt.ylabel("x_1",fontsize=20)
plt.figure(figsize=(15,10))
plot_datasets(x,y)
plt.show()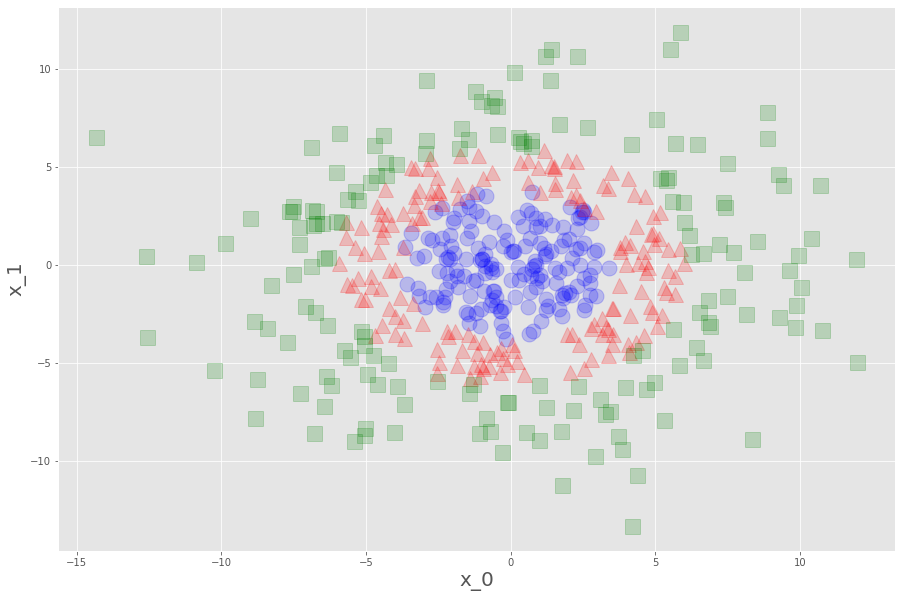
そういうことですね、サイキットラーンさん。ありがとうございます。
cov(デフォルト:1)は共分散の略ですが、公式見る限り特徴量各々の分散です。等方性を持つ分布をつくる、ということなのでどの特徴量の分散も同じ値にするようです。
そうです、こんなんです。この、ザ・線形分離不可の分布が欲しかったんです。
※前回も線形分離不可ですが。
学習と予測平面の描画
ということで、今回もランダムフォレストでもやっていきます。
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import RandomForestClassifier各々こんなハイパーパラメータで学習。
tree=DecisionTreeClassifier(max_depth=10,min_samples_leaf=5).fit(x,y)
rtree=RandomForestClassifier(n_estimators=500,max_depth=40,min_samples_leaf=1).fit(x,y)正解率は、
print(tree.score(x,y))
print(rtree.score(x,y))0.954
1.0ランダムフォレストは
・max_depth=40(細かく領域分けていく)
・min_samples_leaf=1(一つの領域に入るデータの最小数を1にする)
としているので、正解率100%になっています。
過学習なのですが、どんな平面が描かれるのかが見たいのでやります。
まずは決定木(CART)
from matplotlib.colors import ListedColormap
def plot_decision_boundary(clf,x,m=0.2):
_x0=np.linspace(x[:,0].min()-m,x[:,0].max()+m,500)
_x1=np.linspace(x[:,1].min()-m,x[:,1].max()+m,500)
x0,x1=np.meshgrid(_x0,_x1)
x_new=np.c_[x0.ravel(),x1.ravel()]
y_pred=clf.predict(x_new).reshape(x1.shape)
cmap=ListedColormap(["mediumblue","indianred","greenyellow"])
plt.contourf(x0,x1,y_pred,alpha=0.3,cmap=cmap)
plt.figure(figsize=(15,10))
plot_decision_boundary(tree,x)
plot_datasets(x,y)
plt.show()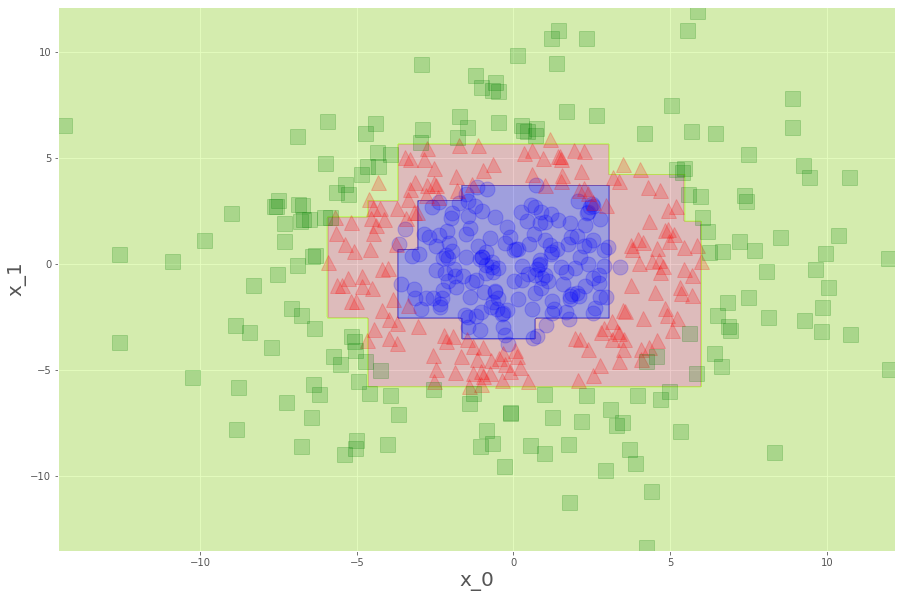
お見事。ランダムフォレストだと、
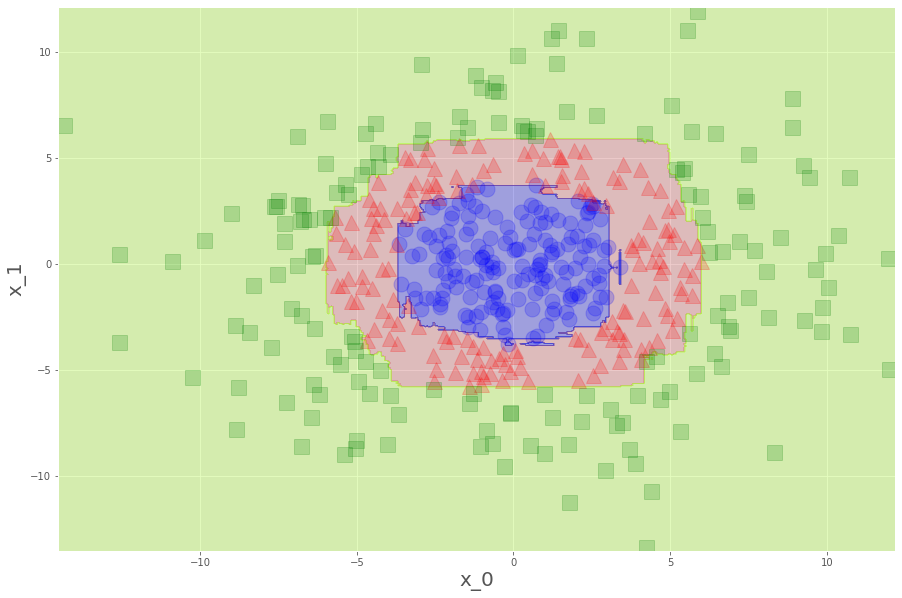
min_samples_leaf=1 なので、1個だけはみ出してるデータまで救って(?)くれています。
ランダムフォレストってすごいね。


