『【Scikit-learn】Olivetti facesデータセットで畳み込みニューラルネットワーク(CNN)してみる』では、層の数/カーネルの数だったり、機械学習には人が決めないといけないハイパーパラメータが大体付いて回ります。これを、いい感じ(低リソースで高精度)に最適なものを見つけ出す、っていうのがOPTUNA(オプチュナ)が実現してくれることです。
どういう理屈?
ほんとに、まったくもってどういう理屈なの?が知りたくて、いろいろ調べたんですけど、
ベースはベイズ最適化という考え方に基づいているとのこと、ほう、それって何だ?
で、ものすごくわかりやすかった記事がこちら、
『ベイズ最適化で期待できること|データ化学工学研究室(金子研究室)@明治大学 理工学部 応用化学科』
なるほど、目から鱗とはこのことですね。
ハイパーパラメータxと最大化(最小化)したい値y、これ、xに対してyが確率分布してるでしょ、
という考え方。まさにベイズ推定の考え方ですね。
- xとyの関数はブラックボックス
- いくつかのxでyを計算
- この結果から、他のxでのyの確率分布(期待値/分散)を計算
- 既知のyよりさらに大きく(小さく)なりうる可能性の高いxを次の計算数値として採用
- 新たにわかった(x,y)も入れて、yの確率分布を更新
ざっくりこんなことと理解しました。確率分布をガウス分布に仮定し、ブラックボックスの関数を回帰することをガウス過程回帰と言うそうです。optunaはガウス過程回帰でなく、また別の手法がとられているようですが。
簡単に使ってみる
理屈をざっくり理解したところで、早速使ってみましょう。
グーグルコラボでやるので、インストールから。
!pip install optunaインストール完了。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use("ggplot")
import optunaいつものと、optunaをインポート。
今回は、わかりやすく探索の過程を見える化したいので、機械学習のハイパーパラメータではなく、適当な関数に対して使ってみようと思います。
$$3x+2sin(x)-4sin^2(x)\\[3pt]+cos(x)+15cos^3(x)+0.3(x-5)(x+5)\\[5pt]+\sqrt{10^2-x^2}
$$
まずは、こんな関数を探索してもらおうと思います。描画するとこんな
x=np.linspace(-10,10,300)
y=3*x+2*np.sin(x)-4*np.sin(x)**2+np.cos(x)+15*np.cos(x)**3+0.3*(x-5)*(x+5)+np.sqrt(100-x**2)
plt.figure(figsize=(10,10))
plt.plot(x,y,lw=5,alpha=0.5,color="black")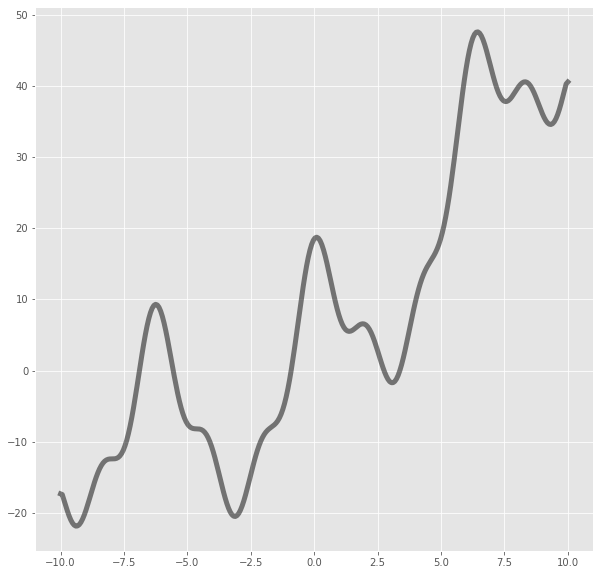
そして、まずはこう。
def objective(trial):
x=trial.suggest_uniform("x",-10,10)
return 3*x+2*np.sin(x)-4*np.sin(x)**2+np.cos(x)+15*np.cos(x)**3+0.3*(x-5)*(x+5)+np.sqrt(100-x**2)trialという引数をもつobjective関数を定義、この中に各ハイパーパラメータの探索範囲や
最大化(最小化)させたい戻り値を書いてあげます。今回は、-10から10で定義された先の関数を
この範囲で探索してね、と書いてます。
study=optuna.create_study()
study.optimize(objective, n_trials=50)そして、これを実行するだけ!むちゃくちゃ簡単ですね。便利すぎる。
n_trialsで探索回数を指定しています。
デフォルトは最小値探索ですが、
study=optuna.create_study(direction="maximize")とすると、最大値を探索してくれます。結果を可視化すると、
plt.figure(figsize=(10,10))
plt.plot([trial.params["x"] for trial in study.trials],
[trial.value for trial in study.trials],
marker="o",ms=8,alpha=0.4,color="red")
plt.scatter(study.trials[0].params["x"], study.trials[0].value,
marker=">",label='start', s=180,color="red")
plt.scatter(study.trials[-1].params["x"],study.trials[-1].value,
marker="x", label="end", s=180,color="red")
plt.scatter(study.best_params["x"], study.best_value,
marker="o",label="best", s=180,color="red")
plt.plot(x,y,lw=5,alpha=0.5,color="black")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="best")
plt.show()
study.best_params, study.best_value({'x': -9.34855148560127}, -21.8190414472504)50回の探索で、最小だったy、そのときのx、はこれで呼び出せます。確かに、最小値あたりを重点的に探索してくれています。グリッドサーチではこうはならないですよね、決めたのを全部計算するので。
次は、半円でやってみます。
$$\sqrt{10^2-x^2}$$
def objective(trial):
x_=trial.suggest_uniform("x_",-10,10)
return np.sqrt(10**2-x_**2)study_=optuna.create_study()
study_.optimize(objective, n_trials=100)x_=np.linspace(-10,10,300)
y_=np.sqrt(10**2-x_**2)plt.figure(figsize=(20,10))
plt.plot([trial.params["x_"] for trial in study_.trials],
[trial.value for trial in study_.trials],
marker="o",ms=8,alpha=0.4,color="red")
plt.scatter(study_.trials[0].params["x_"], study_.trials[0].value,
marker=">",label='start', s=180,color="red")
plt.scatter(study_.trials[-1].params["x_"],study_.trials[-1].value,
marker="x", label="end", s=180,color="red")
plt.scatter(study_.best_params["x_"], study_.best_value,
marker="o",label="best", s=180,color="red")
plt.plot(x_,y_,lw=5,alpha=0.5,color="black")
plt.xlabel("x_")
plt.ylabel("y_")
plt.legend(loc="best")
plt.show()
study_.best_params,study_.best_value({'x_': -9.989239921215322}, 0.46377343218224526)という具合で、最小値を探索してくれました。どちらの0に向かうかは、最初の方にどこのx見るかに依存するのでしょう。
最大値なら、

study_.best_params,study_.best_value({'x_': -0.013870685152540196}, 9.999990380200042)こんな感じ。
x一個なので、分かりやすいですが、当然これ、複数のハイパーパラメータでもoptunaは同じ理屈でやってくれるのです。他にもメリットたくさんあるようですが、今回はこの辺で。


