前回は メイクガウシャンクオンタイルズで生成したデータに対して、決定木による予測平面を描画しました。いいんですけど、境界線がカクカクしてるので(決定木だから当然)、やっぱりなんかこう滑らかな境界線が見たいですよね。となると、そうです、サポートベクトルマシンです。
データの準備
前回と同じデータを使います。
import numpy as np
import matplotlib.pyplot as plt
plt.style.use("ggplot")
from sklearn.datasets import make_gaussian_quantiles
x,y=make_gaussian_quantiles(cov=20,n_samples=500,n_features=2,n_classes=3,random_state=10)
def plot_datasets(x,y):
plt.plot(x[:,0][y==0],x[:,1][y==0],"o",c="blue",ms=15,alpha=0.2)
plt.plot(x[:,0][y==1],x[:,1][y==1],"^",c="red",ms=15,alpha=0.2)
plt.plot(x[:,0][y==2],x[:,1][y==2],"s",c="green",ms=15,alpha=0.2)
plt.xlabel("x_0",fontsize=20)
plt.ylabel("x_1",fontsize=20)
plt.figure(figsize=(15,10))
plot_datasets(x,y)
plt.show()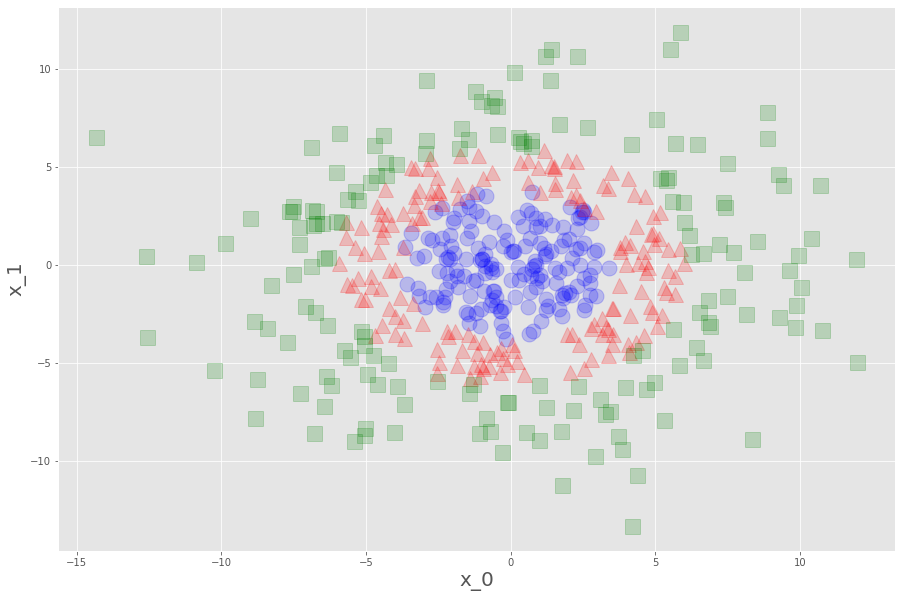
こんなでした。これを学習データとして、決定木とランダムフォレストで予測平面を描くと、
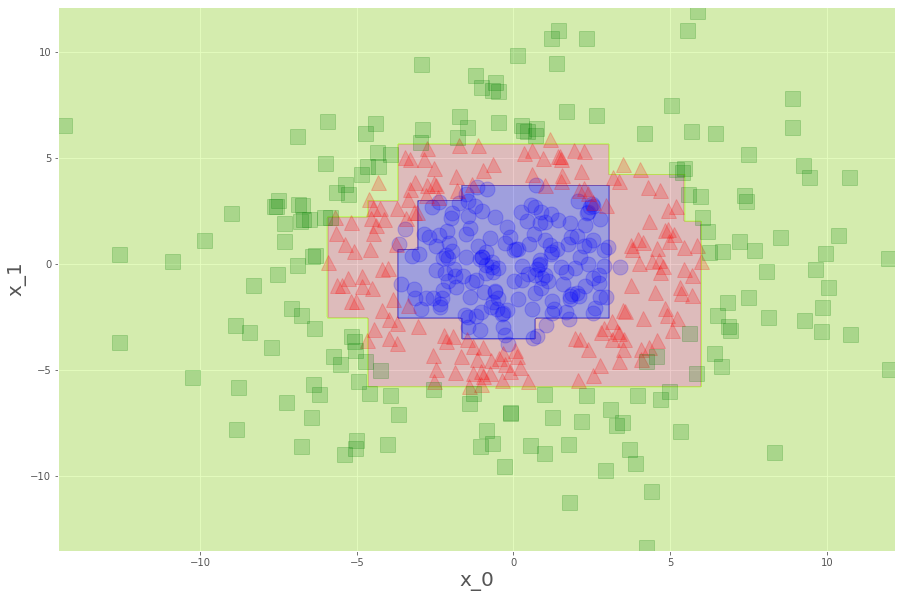
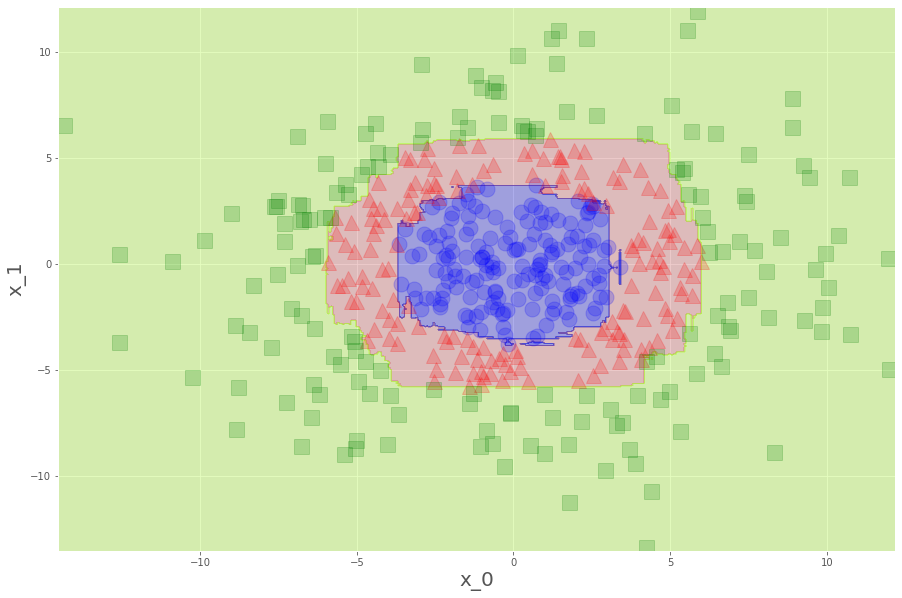
こうでした。見れば見るほど、滑らかな境界線が見たくなります。急ぎましょう。
学習と予測平面の描画
from sklearn.svm import SVC
from sklearn.preprocessing import StandardScaler分類なのでSVCをインポート、標準化するのでスケーラーも。
svm1=SVC(C=1,gamma=0.1)
svm2=SVC(C=10,gamma=1)
svm3=SVC(C=100,gamma=10)おのおのこんなハイパーパラメータにしました。
このパラメータたち、Cは誤判定の影響を決めるパラメータで、まだ理解できます。
ただのこのgamma、これは何でしょう。
線形分離可能にするための高次元量を、式には内積しかでてこないから
ガウシアンカーネルで置き換えるとめっちゃ便利、とのことですが、
理解できる日がくるのでしょうか。
いずれも、大きいとデータにフィットしすぎるやつらです。
scaler=StandardScaler()
x_scaled=scaler.fit_transform(x)標準化して、学習!
svm1.fit(x_scaled,y)
svm2.fit(x_scaled,y)
svm3.fit(x_scaled,y)スコアは各々こんなでした。
print(svm1.score(x_scaled,y))
print(svm2.score(x_scaled,y))
print(svm3.score(x_scaled,y))
0.936
0.982
0.998各々見てみましょう。
plt.figure(figsize=(15,30))
plt.subplot(311)
plot_decision_boundary(svm1,x_scaled)
plot_datasets(x_scaled,y)
plt.title("C=1,gamma=0.1",fontsize=20)
plt.subplot(312)
plot_decision_boundary(svm2,x_scaled)
plot_datasets(x_scaled,y)
plt.title("C=10,gamma=1",fontsize=20)
plt.subplot(313)
plot_decision_boundary(svm3,x_scaled)
plot_datasets(x_scaled,y)
plt.title("C=100,gamma=10",fontsize=20)
plt.show()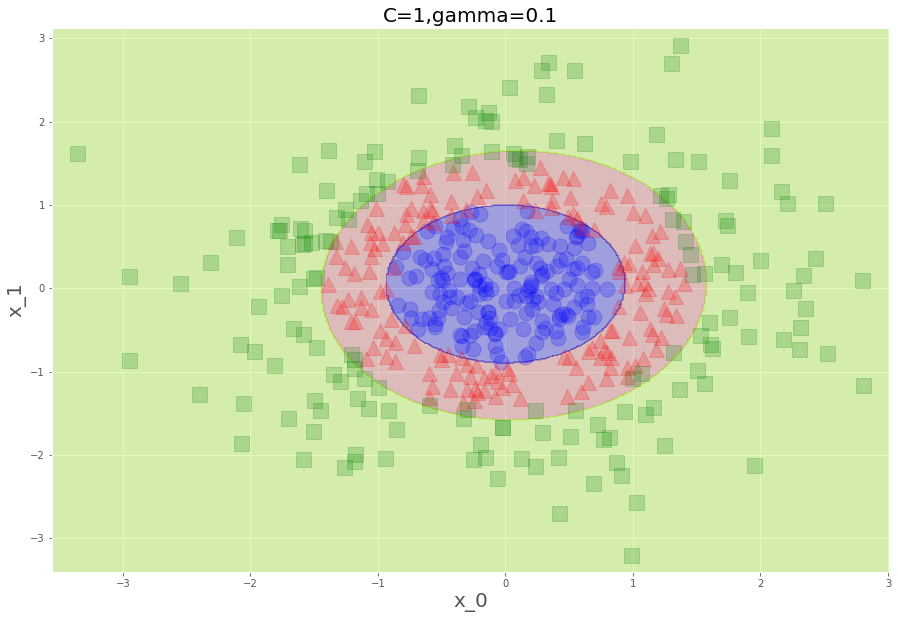
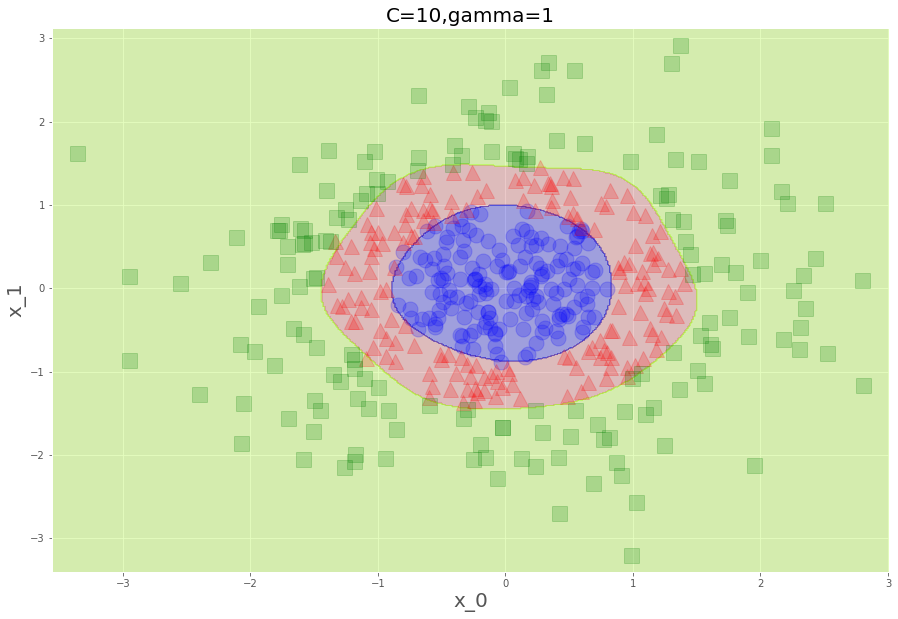

いやー、滑らかって見てて気持ちがいいですね。徐々に崩れていく感じがなんか怖いですけど、実際、下にいくにつれ誤判別許すまじになっています。これが、次元が増えようが何のそので、私たちのPCでチャッチャと動くんですから、ほんとありがたいことです。


